İfadənin mənası “öl”, “öləsən” deməkdir. Keçmişdə igid həlak olanda onun atının yəhərini tərs (arxası qabağa tərəf) qoyub, atı evə buraxırmışlar. Ailədə atı bu vəziyyətdə qarşılayanlar artıq onun sahibsiz qaldığını yəqin edirlərmiş. (Bəşir Əhmədov. Etimologiya lüğəti)

De, Gəlsin!
De, Gəlsin! — 2001-ci ildən 2013-cü ilə qədər Azərbaycanın ANS TV kanalında yayımlanan meyxana yarışma televerilişi.
== İstehsal ==
2001-ci ildən televerilişin introsu meyxana, hip-hop və kapoeyra elementlərindən ibarət olub. Verilişin loqosunun dizaynı "Mortal Kombat" video oyunun əjdaha loqosu üzərində əsaslanıb.
== Tarixi ==
Verilişin qalibləri 2001-ci ildə Aydın Xırdalanlı, 2002-ci ildə Aqşin Fateh və Vüqar Coratlı (III mövsümdə), 2004-cü ildə Vüqar Yasamallı, 2006-cı ildə Namiq Məna, 2008-ci ildə Fariz Bərdəli və 2013-cü ildə Pərviz Arif olub.
== İştirakçılar ==
Rəng açarı
=== Meyxanaçılar ===
=== Ustadlar şurası ===
== İstinadlar ==
== Xarici keçidlər ==
De, Gəlsin!

Yəhərli (Tikantəpə)
Yəhərli (fars. يهرلو) — İranın Qərbi Azərbaycan ostanının Tikantəpə şəhristanı ərazisinə daxil olan kənd.
2006-cı il məlumatına görə kənddə 253 nəfər yaşayır (53 ailə).

Yəhərli tapir
Yəhərli tapir (lat. Tapirus indicus)) — Təkdırnaqlılar dəstəsinin Tapirkimilər fəsiləsinin tapir cinsinə aid heyvan növü. İki yarımnövə ayrılır: Hartman dağ zebri (Equus zebr hartmannae) və Equus zebr zebr.
Tapirlər arasında ən böyüyü hesab olunur. Bədəninin uzunluğu 1,8-2,4 m, süysününün hündürlüyü 0,75–1 m, kütləsi 250-320 kq olur. İndiyədək məlum olan ən böyük yəhərli tapirin kütləsi 540 kq olub.

Tərs funksiya
Tutaq ki,
y
=
f
(
x
)
{\displaystyle y=f(x)}
,
x
∈
D
(
f
)
{\displaystyle x\in D(f)}
ədədi funksiya verilmişdir. Onda hər bir
x
0
∈
D
(
f
)
{\displaystyle x_{0}\in D(f)}
ədədinə yeganə
y
0
=
f
(
x
0
)
∈
E
(
f
)
{\displaystyle y_{0}=f(x_{0})\in E(f)}
ədədi uyğundur. Funksiyanın verilən
y
0
{\displaystyle y_{0}}
qiymətinə görə arqumentin uyğun qiymətinin tapılmasına, daha doğrusu
f
(
x
)
=
y
0
{\displaystyle f(x)=y_{0}}
,
y
0
∈
E
(
f
)
{\displaystyle y_{0}\in E(f)}
tənliyinin
x
{\displaystyle x}
-ə nəzərən həllinə tez-tez rast gəlinir. Həmin tənliyin bir yox, bir neçə və hətta sonsuz sayda həlli ola
bilər.
y
=
f
(
x
)
{\displaystyle y=f(x)}
funksiyasının qrafiki ilə
y
=
y
0
{\displaystyle y=y_{0}}
düz xəttinin kəsişdiyi bütün nöqtələrin absisləri
f
(
x
)
=
y
0
{\displaystyle f(x)=y_{0}}
tənliyinin
Əgər
f
{\displaystyle f}
funksiyası hər bir
y
0
∈
E
(
f
)
{\displaystyle y_{0}\in E(f)}
qiymətini ancaq yeganə bir
x
0
∈
D
(
f
)
{\displaystyle x_{0}\in D(f)}
qiymətində alırsa, onda o
funksiya dönən adlanır. Belə funksiyalar üçün
f
(
x
)
=
y
{\displaystyle f(x)=y}
tənliyini istənilən
y
∈
E
(
f
)
{\displaystyle y\in E(f)}
qiymətində x-ə nəzərən birqiymətli həll etmək olar, daha doğrusu hər bir
y
∈
E
(
f
)
{\displaystyle y\in E(f)}
qiymətinə yeganə
x
∈
D
(
f
)
{\displaystyle x\in D(f)}
qiyməti uyğundur. Bu uyğunluq funksiya təyin edir, özü də
f
{\displaystyle f}
funksiyasının tərsi
adlanır və
f
−
1
{\displaystyle f^{-1}}
simvolu ilə işarə olunur.
Qeyd edək ki, hər bir
y
0
∈
E
(
f
)
{\displaystyle y_{0}\in E(f)}
üçün
y
=
y
0
{\displaystyle y=y_{0}}
düz xətti dönən
y
=
f
(
x
)
{\displaystyle y=f(x)}
funksiyasının qrafikini yeganə
(
x
0
,
y
0
)
{\displaystyle (x_{0},y_{0})}
nöqtəsində kəsir, burada
f
(
x
0
)
=
y
0
{\displaystyle f(x_{0})=y_{0}}
.
Tərs funksiyanın arqumentini
x
{\displaystyle x}
hərfi ilə, onun qiymətini isə –
y
{\displaystyle y}
hərfi ilə işarə edərək,
f
{\displaystyle f}
funksiyasının
tərs funksiyasını
y
=
f
−
1
(
x
)
,
x
∈
D
(
f
−
1
)
{\displaystyle y=f^{-1}(x),x\in D(f^{-1})}
,
şəklində yazırlar. Sadəlik üçün
f
−
1
{\displaystyle f^{-1}}
simvolu əvəzinə
g
{\displaystyle g}
hərfindən istifadə edəcəyik.
Tərs matris
Tərs matris — n tərtibli A kvadrat matrisinin tərsi elə bir B matrisinə deyilirki,
A
B
=
B
A
=
E
n
{\displaystyle AB=BA=E_{n}}
şərti ödənilsin. Burada En, n tərtibli vahid matrisdir.
E
n
=
(
1
0
⋯
0
0
1
⋯
0
⋮
⋮
⋱
⋮
0
0
⋯
1
)
{\displaystyle E_{n}={\begin{pmatrix}\mathbf {1} &\mathbf {0} &\cdots &\mathbf {0} \\\mathbf {0} &\mathbf {1} &\cdots &\mathbf {0} \\\vdots &\vdots &\ddots &\vdots \\\mathbf {0} &\mathbf {0} &\cdots &\mathbf {1} \\\end{pmatrix}}}
Tərs matrisi B=A−1 kimi işarələyirlər. Buradan belə nəticəyə gəlmək olar ki,
A
A
−
1
=
A
−
1
A
=
E
n
{\displaystyle A{A^{-1}}=A^{-1}A=E_{n}}
bərabərlik şərti ödənilməlidir.

Tərs qəfəs
Tərs qəfəs-mücərrəd üçölçülü bir fəzada qurulmuş nöqtəvi qəfəsdir. Bunun hansı fəzada necə qurulduğunu və ümumiyyətlə nəyə yaradığını yaxşı anlamaq üçün tərs qəfəs anlayışının bərk cisimlər fizikasındakı roluna nəzər salaq.
Kristallik bərk cisimlərin bütün fiziki xassələri, əsas etibarı ilə iki faktor əsasında formalaşır. Bunlardan biri bərk cismi təşkil edən atomların quruluşu, ikincisi isə bərk cisimlərin öz kristal quruluşudur. Bir bərk cismin kristal quruluşa sahib olması nəzəri problemlərin həllində xüsusi əhəmiyyət kəsb edir. Beləki bərk cismin fiziki xassəsini ifadə edən və koordinatın funksiyası olan hər bir fiziki kəmiyyət koordinatın üçölçülü periodik funksiyası olur. Bu o deməkdir ki, bir nəzəri məsələnin həlli üçün yazılacaq tənliklərin bərk cismi təşkil edən bütün atomlar üçün deyil, periodun müəyyən elədiyi oblastda yer alan atomlar üçün yazılması kifayətdir. Period isə kristal qəfəsin köçürmə simmetriyasını müəyyən edən
a
→
1
,
a
→
2
,
a
→
3
{\displaystyle {\vec {a}}_{1},{\vec {a}}_{2},{\vec {a}}_{3}}
vektorları ilə verilir. Bu vektorlara qəfəsin bazis vektorları və onların ədədi qiymətləri olan
a
,
b
,
c
{\displaystyle a,b,c}
-lərə qəfəs sabitləri deyilir. Hər bir qəfəs üçün
a
→
i
{\displaystyle {\vec {a}}_{i}}
vektorları üzərində qurulumuş paralepiped həmin qəfəsin elementar özəyi adlanır və onun həcmi
V
0
=
(
a
→
1
[
a
→
2
a
→
3
]
)
{\displaystyle V_{0}={\Bigl (}{\vec {a}}_{1}[{\vec {a}}_{2}{\vec {a}}_{3}]{\Bigr )}}
.

Tərs yer
Tərs yer — Azərbaycan Respublikasının Gədəbəy rayonunun inzibati ərazi vahidində kənd. Azərbaycan Respublikası Milli Məclisinin 5 oktyabr 1999-cu il tarixli, 708-IQ saylı Qərarı ilə Gədəbəy rayonunun Samanlıq kənd inzibati-ərazi vahidi tərkibindəki yaşayış məntəqəsi Tərs yer kəndi adlandırılmış və rayonun yaşayış məntəqələri uçot məlumatına daxil edilmişdir.
Kənd Kiçik Qafqaz dağlarının ətəyində, dağlıq ərazidə yerləşir.
2009-cu ilin siyahıyaalınmasına əsasən kənddə 138 nəfər əhali yaşayır.
Əhalinin əsas məşğuliyyətini kənd təsərrüfatı — əkinçilik, maldarlıq və heyvandarlıq təşkil edir.

Tərs çay
Tərs çay və ya Tərs çay qışlağı - Yelizavetpol (Gəncə) quberniyasının Qazax qəzasında, Dilican şəhəri yaxınlığında qışlaq.
Tərsa çayının sahilində salındığı üçün yaşayış məntəqəsinin adı «Tərs çay qışlağı» adlandırılmışdır. Hidrotoponimdir. Quruluşca mürəkkəb toponimdir.
1897-ci ildə burada 10 nəfər azərbaycanlı, 18 erməni, 4 rus yaşamışdır.
XX əsrin əvvəllərində ləğv edilmişdir.

Tərs A
Tərs A (böyük Ɐ, kiçik ɐ, riyazi simvol ∀) – A hərfinin tərsinə çevrilməsi ilə yaranan hərf və simvol.
ɐ hərfi beynəlxalq fonetik əlifbada istifadə olunan simvollardan biridir.
∀ simvolu riyaziyyatda universal kvantifikasiyanı bildirmək üçün istifadə olunan məntiq simvoludur və "hamısı üçün" kimi tərcümə olunur. İlk dəfə Qerhard Qentsen tərəfindən 1935-ci ildə istifadə olunmuşdur. O, ilk dəfə Cüzeppe Peano tərəfindən istifadə olunmuş Ǝ simvolundan ilhamlanmışdır.
Tərs a hərfi Edvard Lluyd və Vilyam Prays tərəfindən Korn dili üçün fonetik simvol kimi istifadə olunmuşdur. Onların kitablarında Ɐ və ɐ simvolları istifadə olunmuşdur. Simvol XIX əsrdə riyaziyyatçı Çarlz Sanders tərəfindən məntiq simvolu kimi işlədilmişdir. 2023-cü ildə Azərbaycan ordusuna məxsus hərbi texnikanın üzərində yazılmış tərsinə A hərfi Ermənistanda Zəngəzur dəhlizinə müdaxilənin simvolu kimi qiymətləndirilsə də, Azərbaycan tərəfi bu simvolun sadəcə digər ölkəyə aid maşınlardan fərqləndirmək üçün istifadə olunduğunu bildirmişdir.
Akrofoniya prinsipinə görə A hərfi protosinan yazısında öküz (alef) başını təmsil edən simvoldan yaranmışdır.

Tərs mühəndislik
Tərsinə mühəndislik — deduktiv mülahizə vasitəsilə əvvəllər hazırlanmış cihazın, prosesin, sistemin və ya proqram təminatının bir tapşırığı necə yerinə yetirdiyinin (əgər varsa) başa düşülməyə çalışıldığı proses və ya üsul. Nəzərdən keçirilən sistemdən və istifadə olunan texnologiyalardan asılı olaraq, tərsinə mühəndislik zamanı əldə edilən biliklər köhnəlmiş obyektlərin təyinatının dəyişdirilməsinə, təhlükəsizlik analizinin aparılmasına və ya bir şeyin necə işlədiyini öyrənməyə kömək edə bilər.
Prosesin həyata keçirildiyi obyektə xas olmasına baxmayaraq, bütün tərsinə mühəndislik prosesləri üç əsas addımdan ibarətdir: məlumatın çıxarılması, modelləşdirmə və nəzərdən keçirmə. Məlumat çıxarma əməliyyat üçün bütün müvafiq məlumatların toplanması təcrübəsidir. Modelləşdirmə, yeni bir obyekt və ya sistemin layihələndirilməsi üçün bələdçi kimi istifadə edilə bilən abstrakt bir modeldə toplanmış məlumatların birləşdirilməsi təcrübəsidir. Nəzərdən keçirmə seçilmiş abstraktın etibarlılığını təmin etmək üçün modelin sınaqdan keçirilməsidir. Tərsinə mühəndislik kompüter mühəndisliyi, maşınqayırma, dizayn, elektron mühəndislik, proqram mühəndisliyi, kimya mühəndisliyi və sistem biologiyası sahələrində tətbiq olunur.
Müxtəlif sahələrdə tərsinə mühəndisliyi yerinə yetirməyin bir çox səbəbi var. Tərsinə mühəndislik öz mənşəyini kommersiya və ya hərbi üstünlük üçün aparatların analizindən alır.:13 Bununla belə, tərsinə mühəndislik prosesi həmişə surətin yaradılması və ya artefaktın hansısa şəkildə dəyişdirilməsi ilə bağlı olmaya bilər.:15
Bəzi hallarda tərsinə mühəndislik prosesinin məqsədi sadəcə olaraq köhnə sistemlərin yenidən sənədləşdirilməsi ola bilər.:15 Hətta tərsinə çevrilmiş məhsul rəqibin məhsulu olsa belə, məqsəd onu kopyalamaq deyil, rəqibin analizini aparmaq ola bilər. Tərsinə mühəndislik qarşılıqlı fəaliyyət göstərən məhsullar yaratmaq üçün də istifadə edilə bilər və bəzi dar çərçivədə hazırlanmış ABŞ və Avropa İttifaqı qanunvericiliyinə baxmayaraq, bu məqsədlə xüsusi tərsinə mühəndislik üsullarından istifadənin qanuniliyi iyirmi ildən artıqdır ki, bütün dünyada məhkəmələrdə qızğın mübahisələrə səbəb olur.

Tərs piramida
Tərs Piramida (ing. PR – inverted pyramid) jurnalistikada, kopiraytinqdə və reklam yazarlığında tez-tez istifadə olunan termindir. Akademik yazılardan fərqli olaraq xəbər və ya reklam mətnləri Düz piramida deyil, "Tərs Piramida" formatında yazılır. "Tərs Piramida" qaydasına görə, ən vacib informasiya mətnin əvvəlində, yəni ilk cümlədə verilir. Sonra mətnin təfərrüatı və sonda "background" (arayış) deyilən hissə əlavə olunur. Bu prinsip ilə yazılan mətnlər dərhal oxucunun diqqətini cəlb edir.[1]
Xəbər və reklam mətnlərində ən vacib informasiya mətnin əvvəlində olmalıdır. Məhz bu prinsipə "tərs piramida" deyilir.
Məktəb və universitetlərdə bizə mətnlərin sadədən mürəkkəbə doğru yazılmasını öyrədirlər. Mətnlər yüngül məlumatlardan başlanır, tədricən qəlizləşir. Bu, mətn yazılmasında "düz piramida" prinsipidir.
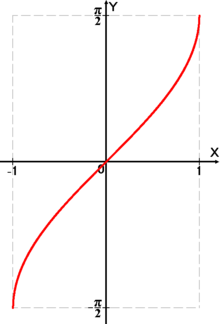
Tərs triqonometrik funksiyalar
Tərs triqonometrik funksiyalar (dairəvi funksiya, arkfunksiya) — triqonometrik funksiyalar tərsinə çevrilə bilən riyazi funksiyalardır. Tərs triqonometrik funksiyalara əsasən altı funksiya daxildir:
arksinus (
a
r
c
s
i
n
x
{\displaystyle \mathrm {arcsin} \,x}
— bu bucağın sinusu
x
{\displaystyle x}
-ə bərabərdir)
arkkosinus (
a
r
c
c
o
s
x
{\displaystyle \mathrm {arccos} \,x}
— bu bucağın kosinusu
x
{\displaystyle x}
-ə bərabərdir)
arktangens (
a
r
c
t
a
n
x
{\displaystyle \mathrm {arctan} \,x}
, bəzi ədəbiyyatlarda
a
r
c
t
g
x
{\displaystyle \mathrm {arctg} \,x}
)
arkkotangens (
a
r
c
c
o
t
x
{\displaystyle \mathrm {arccot} \,x}
və ya
a
r
c
c
o
t
a
n
x
{\displaystyle \mathrm {arccotan} \,x}
, bəzi ədəbiyyatlarda
a
r
c
c
t
g
x
{\displaystyle \mathrm {arcctg} \,x}
)
arksekans (
a
r
c
s
e
c
x
{\displaystyle \mathrm {arcsec} \,x}
)
arkkosekans (
a
r
c
c
s
c
x
{\displaystyle \mathrm {arccsc} \,x}
, bəzi ədəbiyyatlarda
a
r
c
c
o
s
e
c
x
{\displaystyle \mathrm {arccosec} \,x}
)
Triqonometrik funksiyaların adının qarışındakı "arc" sözü ( lat. arcus — ox, qövs, qövsəoxşar xətt) bu funksiyaları tərs triqonometrik funksiyaların adına çevirir. Bu onunla bağlıdır ki, tərs triqonometrik funksiyaların həndəsi qiyməti vahid çevrənin qövsünün uzunluğu ilə əlaqələndirmək olar. Tərs triqonometrik funksiyalar anlayışını Laqranj köməyi ilə Avstriya riyaziyyatçısı Karla Şerfer (alm. Karl Scherffer; 1716—1783) daxil etmişdir.
arcsin
x
+
arccos
x
=
π
2
{\displaystyle \arcsin x+\arccos x={\frac {\pi }{2}}}
arctan
x
+
arccot
x
=
π
2
{\displaystyle \operatorname {arctan} \,x+\operatorname {arccot} \,x={\frac {\pi }{2}}}
Arksinus - m ədədinin x bucağının qiymətinə , radian ifadəsinə deyilir, hansı ki,
sin
x
=
m
,
−
π
2
⩽
x
⩽
π
2
,
|
m
|
⩽
1.
{\displaystyle \sin x=m,\,-{\frac {\pi }{2}}\leqslant x\leqslant {\frac {\pi }{2}},\,|m|\leqslant 1.}
y
=
sin
x
{\displaystyle y=\sin x}
funksiyası bütün ədəd oxunda kəsilməz və məhduddur.
y
=
arcsin
x
{\displaystyle y=\arcsin x}
funksiyası ciddi artandır.
sin
(
arcsin
x
)
=
x
{\displaystyle \sin(\arcsin x)=x\qquad }
−
1
⩽
x
⩽
1
,
{\displaystyle -1\leqslant x\leqslant 1,}
arcsin
(
sin
y
)
=
y
{\displaystyle \arcsin(\sin y)=y\qquad }
−
π
2
⩽
y
⩽
π
2
,
{\displaystyle -{\frac {\pi }{2}}\leqslant y\leqslant {\frac {\pi }{2}},}
D
(
arcsin
x
)
=
[
−
1
;
1
]
{\displaystyle D(\arcsin x)=[-1;1]\qquad }
(təyin oblastı),
E
(
arcsin
x
)
=
[
−
π
2
;
π
2
]
{\displaystyle E(\arcsin x)=\left[-{\frac {\pi }{2}};{\frac {\pi }{2}}\right]\qquad }
(qiymətlər çoxluğu).

Tərs yumurtavari səna
Əsasən Sudanda yayılmışdır.
Hündürlüyü 1 metr olan yarımkol və ya koldur. Yarpaqları 5 cüt, yarpaqcıqları enli, tərs-yumurtavari, ucdan dəyirmidir. Ləçəkləri qeyri bərabərdir. Paxlası yastı, oraqvari, iri, 3-4 sm uzunluğundadır. Avqust ayında çiçəkləyir.
İşığa, istiyə, küləyədavamlı bitkidir. Torpağa tələbkar deyildir.
Mədəni halda Abşeronda Dendrologiya İnstitutunun təcrübə sahəsində becərilir.
Yolların kənarlarında canlı çəpərlərin salınmasında, qrup əkinlərində istifadəsi məqsədyönlüdür.

De, Gəlsin! (veriliş, 2001)
De, Gəlsin! — 2001-ci ildən 2013-cü ilə qədər Azərbaycanın ANS TV kanalında yayımlanan meyxana yarışma televerilişi.
== İstehsal ==
2001-ci ildən televerilişin introsu meyxana, hip-hop və kapoeyra elementlərindən ibarət olub. Verilişin loqosunun dizaynı "Mortal Kombat" video oyunun əjdaha loqosu üzərində əsaslanıb.
== Tarixi ==
Verilişin qalibləri 2001-ci ildə Aydın Xırdalanlı, 2002-ci ildə Aqşin Fateh və Vüqar Coratlı (III mövsümdə), 2004-cü ildə Vüqar Yasamallı, 2006-cı ildə Namiq Məna, 2008-ci ildə Fariz Bərdəli və 2013-cü ildə Pərviz Arif olub.
== İştirakçılar ==
Rəng açarı
=== Meyxanaçılar ===
=== Ustadlar şurası ===
== İstinadlar ==
== Xarici keçidlər ==
De, Gəlsin!

Tərs siyahılı verilənlər bazası
Tərs siyahılı verilənlər bazası ( ing. inverted list database ~ ru. база данных инвертированного списка ~ tr. ters listeli veritabanı) – relyasiyalı verilənlər bazasından aşağıdakı fərqləri olan verilənlər bazası:
• Tərsinə çevrilmış siyahı cədvəlinin sətirləri (yazıları və ya kortejləri) hər hansı indeksləmə ardıcıllığından asılı olmayaraq müəyyən fiziki ardıcıllıqla yerləşir.
• Ümumi verilənlər bazasını, bazanın cədvəlləri üçün qurulmuş müəyyən məntiqi birləşdirmə meyarlarından istifadə etməklə nizamlamaq olar.
• Siyahının açarlarının sayı istənilən qədər ola bilər, həm də istər sadə, istərsə də mürəkkəb açarların əksinə olaraq, burada onlar istənilən sahə və ya sahələrin kombinasiyası ola bilər.
• Bütövlüyə və ya unikallığa heç bir məhdudiyyət yoxdur.
• Nə indekslər, nə də cədvəllər istifadəçiyə göstərilir.
Belə verilənlər bazasının idarə olunması sistemindəki bu fərqlərə görə verilənlərin uzlaşmasını, bütövlüyünü və təhlükəsizliyini təmin etmək çox çətindir.
İsmayıl Calallı (Sadıqov), “İnformatika terminlərinin izahlı lüğəti”, 2017, “Bakı” nəşriyyatı, 996 s.